|
К содержанию Ореховский П. А., Дьяченко А. П., Сухинин И. В.
Оценка влияния экзогенных и эндогенных факторов на механизм циклов Кондратьева
(промежуточный отчет по гранту).
III. Гипотезы и обоснование корректности расчетов
Собственно, основной гипотезой, которую предполагалось подтвердить или опровергнуть статистическими исследованиями, осуществляемыми в ходе реализации проекта, являлось предположение о доминирующем влиянии экзогенных факторов на механизм реализации циклов Кондратьева в “отдельно взятой” национальной экономике. Циклы Кондратьева, пожалуй, самый крупный известный науке феномен долгосрочной экономической динамики. Соответственно, доказательство вышеприведенного положения позволяет сделать вывод о решающей роли экзогенных факторов в экономическом развитии вообще, о чем уже говорилось в первой части нашего отчета.
Статистическая проверка, таким образом, распадается на две части: исследование “длинных волн” в рядах приведенных выше показателей и определение степени корреляции между экономическим развитием в разных странах. Поскольку речь идет об экономической динамике, необходимо исследовать темпы прироста номинальных показателей, что позволяет добиться сравнимости динамики различных стран независимо от того, в каких денежных единицах, к какому базисному году были привязаны исходные ряды. Кроме того, поскольку часть показателей приведена в относительных единицах, их также можно перевести в темпы прироста. Поскольку речь идет о цепных индексах, верность такого преобразования можно продемонстрировать на примере следующих преобразований:
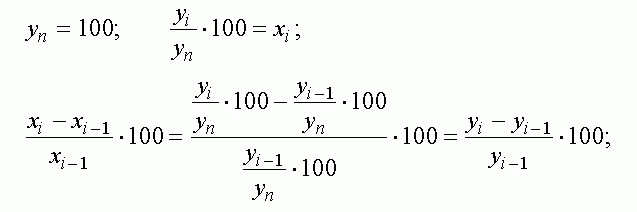
где хi – относительные показатели;
yi – абсолютные показатели;
yn – значение показателя в базисном году.
Таким образом сравнение динамики абсолютных показателей и относительных вполне корректно.
В то же время следует сделать оговорку: на этом этапе исследования, поскольку данные о населении и занятости являются по некоторым странам весьма обрывочными, анализу подвергались темпы прироста, не взвешенные по населению (в противном случае сделаны специальные оговорки). Таблицы с рассчитанными темпами прироста приводятся ниже.
Таблица 9. Динамика изменений в производстве промышленной продукции по странам (1900 – 1994)
| | Англия | США | Франция | Германия | Италия | Япония | Канада | Россия |
| 1901 | 1,476 | 9,494 | -5,6 | -2,74 | 0 | 3,371 | | 3,846 |
| 1902 | 1,818 | 2,023 | 4,5 | 1,408 | 9,302 | -3,261 | | 3,704 |
| 1903 | -1,429 | 17,28 | 1,4 | 8,333 | 0 | 1,124 | | 7,143 |
| 1904 | 1,812 | 1,691 | 4,2 | 5,128 | 4,255 | -1,111 | | 0 |
| 1905 | 3,915 | 18,765 | 2,7 | 2,439 | 6,122 | 3,371 | | 13,333 |
| 1906 | 2,397 | 4 | 2,6 | 4,762 | 11,538 | 8,696 | | 8,824 |
| 1907 | 2,676 | 11,538 | 6,4 | 7,955 | 8,621 | 10 | | 5,405 |
| 1908 | -3,257 | -12,069 | 0 | -1,053 | 3,175 | 0 | | -7,692 |
| 1909 | 1,684 | 17,647 | 7,2 | 4,255 | 3,077 | 0 | | 11,111 |
| 1910 | 1,656 | 8,333 | 7,9 | 6,122 | 0 | 9,091 | | 7,5 |
| 1911 | 3,909 | 0 | 3,1 | 5,769 | 0 | 8,333 | | 2,326 |
| 1912 | 2,821 | 9,231 | 9,1 | 6,364 | 7,463 | 7,692 | | 6,818 |
| 1913 | 3,659 | 5,634 | 0 | 2,564 | -2,778 | 14,286 | | -8,511 |
| 1914 | | -6,667 | 7,9 | -19,167 | -4,286 | -6,25 | | 2,326 |
| 1915 | | 11,429 | 6,9 | -11,34 | 29,851 | 13,333 | | 15,909 |
| 1916 | | 19,231 | 11,2 | 18,605 | 0 | 17,647 | | 3,922 |
| 1917 | | 6,452 | 0 | 5,882 | -10,345 | 15 | -44,964 | -1,887 |
| 1918 | | 0 | -40,1 | -14,815 | -3,846 | 8,696 | -25,49 | -15,385 |
| 1919 | | -4,04 | -25,9 | -58,261 | -2,667 | 4 | -46,491 | -84,091 |
| 1920 | | 5,263 | 8,1 | 77,083 | 0 | -7,692 | 40,984 | 0 |
| 1921 | -12,226 | -23 | -10,5 | 29,412 | -8,219 | 8,333 | 31,395 | 42,857 |
| 1922 | 7,5 | 27,273 | 41,2 | -3,409 | 11,94 | 3,846 | 53,097 | 30 |
| 1923 | 3,322 | 19,388 | 13,1 | -37,647 | 8 | 0 | 16,763 | 46,154 |
| 1924 | 5,145 | -5,983 | 22,6 | 49,057 | 11,111 | 3,704 | 65,347 | 21,053 |
| 1925 | 2,752 | 9,091 | -0,9 | 56,962 | 13,333 | 10,714 | 43,413 | 65,217 |
| 1926 | -2,083 | 6,667 | 17,3 | -10,484 | 0 | 6,452 | | 42,105 |
| 1927 | 8,511 | -0,781 | -12,5 | 28,829 | -2,941 | 6,061 | | 62,963 |
| 1928 | 0 | 4,724 | 0,8 | 0 | 9,091 | 2,857 | | -30,682 |
| 1929 | 2,521 | 10,526 | 10 | 0,699 | 2,778 | 8,333 | | 14,754 |
| 1930 | -1,366 | -17,007 | 0 | -12,5 | -5,405 | 0 | 42,857 | 30 |
| 1931 | -3,601 | -17,213 | -13,8 | -19,048 | -9,524 | -7,692 | -20 | 108,791 |
| 1932 | 0,287 | -20,792 | -14,5 | -13,725 | 0 | 5,556 | -12,5 | 10,526 |
| 1933 | 4,011 | 16,25 | 9,3 | 12,5 | 6,316 | 21,053 | 14,286 | 4,762 |
| 1934 | 5,51 | 9,677 | -6,6 | 23,232 | -1,98 | 6,522 | 25 | 22,727 |
| 1935 | 4,439 | 15,686 | -4 | 18,033 | 7,071 | 6,122 | 10 | 22,222 |
| 1936 | 5,5 | 17,797 | 7,4 | 13,889 | 0 | 13,462 | 9,091 | 27,273 |
| 1937 | 3,791 | 9,353 | 5,9 | 11,585 | 16,038 | 16,949 | 8,333 | 11,905 |
| 1938 | -1,37 | -32,895 | -8,3 | 9,836 | 0 | 2,899 | -15,385 | 10,638 |
| 1939 | -4,861 | 23,529 | 21,2 | -4,975 | 8,943 | 9,859 | 18,182 | 15,385 |
| 1940 | | 34,921 | -100 | | 1,493 | 5,128 | 23,077 | 16,667 |
| 1941 | | 26,471 | | | -6,618 | 3,659 | 18,75 | -1,429 |
| 1942 | | 14,884 | | | -13,386 | -3,529 | 21,053 | -21,739 |
| 1943 | | 21,862 | -11,6 | | -22,727 | 1,22 | 4,348 | 16,667 |
| 1944 | | 6,977 | -29,9 | | -38,824 | 2,41 | 0 | 14,286 |
| 1945 | | -13,975 | 32 | | -30,769 | -56,471 | -12,5 | -16,667 |
| 1946 | | -14,079 | 67,7 | | 141,667 | -54,054 | -9,524 | -16,667 |
| 1947 | 1,101 | 12,605 | 18,1 | 17,857 | 28,736 | 23,529 | 10,526 | 20 |
| 1948 | 4,575 | 4,478 | 14,3 | 53,03 | 8,929 | 28,571 | 4,762 | 33,333 |
| 1949 | 3,542 | -5,714 | 7,6 | 47,525 | 8,197 | 29,63 | 0 | 25 |
| 1950 | 3,622 | 15,53 | 5 | 24,832 | 15,909 | 20 | 13,636 | -20 |
| 1951 | 1,748 | 8,525 | 11,9 | 19,892 | 13,725 | 35,714 | 4 | 25 |
| 1952 | -0,573 | 3,927 | 1,4 | 7,175 | 1,149 | 7,018 | 3,846 | 10 |
| 1953 | 4,031 | 8,43 | 0,7 | 6,695 | 10,227 | 21,311 | 7,407 | 9,091 |
| 1954 | 4,244 | -5,362 | 8,7 | 14,51 | 8,763 | 8,108 | -3,448 | 16,667 |
| 1955 | 3,363 | 12,748 | 8,3 | 12,671 | 10,427 | 12,5 | 10,714 | 28,571 |
| 1956 | 1,027 | 4,523 | 9,4 | 8,207 | 6,867 | 23,333 | 12,903 | -5,556 |
| 1957 | 1,695 | 1,202 | 8,3 | 5,899 | 6,827 | 16,216 | 0 | 5,882 |
| 1958 | -0,167 | -6,413 | 4,5 | 2,918 | 5,639 | -0,775 | 0 | 11,111 |
| 1959 | 4,674 | 11,929 | 3,3 | 6,959 | 9,253 | 19,531 | 8,571 | 10 |
| 1960 | 5,263 | 2,041 | 10,1 | 11,325 | 15,309 | 23,529 | 0 | 9,091 |
| 1961 | 1,818 | 0,889 | 4,8 | 6,926 | 11,017 | 17,989 | 2,632 | 12,5 |
| 1962 | 1,488 | 8,15 | 7,6 | 4,453 | 9,924 | 8,52 | 7,692 | 7,407 |
| 1963 | 3,226 | 5,906 | 2,2 | 2,907 | 8,565 | 9,917 | 4,762 | 10,345 |
| 1964 | 6,108 | 6,923 | 8,9 | 7,721 | 1,919 | 129,699 | 9,091 | 6,25 |
| 1965 | 2,811 | 9,892 | 2 | 7,168 | 5,021 | 2,455 | 16,667 | 8,824 |
| 1966 | 1,693 | 8,838 | 6,9 | 1,305 | 11,155 | -41,214 | 7,143 | |
| 1967 | 1,793 | 2,256 | 2,4 | -2,576 | 7,527 | 19,293 | 0 | |
| 1968 | 4,277 | 6,324 | 3,4 | 12,231 | 6,333 | 17,312 | 6,667 | 9,091 |
| 1969 | 1,93 | 4,564 | 11,1 | 11,929 | 2,978 | 26,602 | 7,813 | 8,333 |
| 1970 | 1,775 | -3,042 | 5,4 | 7,632 | 7,763 | 2,147 | 1,449 | 7,692 |
| 1971 | 1,395 | 1,774 | 5,3 | 1,956 | 0 | 2,703 | 5,714 | 7,143 |
| 1972 | 3,211 | 9,115 | 2,6 | 3,957 | 4,237 | 7,31 | 6,757 | 6,667 |
| 1973 | 5,778 | 8,477 | 6,5 | 6,574 | 9,485 | 17,575 | 8,861 | 7,813 |
| 1974 | -1,471 | -0,34 | 1,7 | -1,84 | 4,703 | -6,025 | 2,326 | 7,246 |
| 1975 | -1,919 | -8,977 | -6 | -6,615 | -9,102 | -10,481 | -10,227 | 8,108 |
| 1976 | 2,065 | 10,861 | 6,4 | 8,028 | 12,094 | 11,019 | 13,924 | 5 |
| 1977 | 2,769 | 5,856 | 0,8 | 2,842 | -1,74 | 4,094 | 3,333 | 7,143 |
| 1978 | 3,523 | 5,745 | 0,8 | 0,85 | 5,313 | 6,436 | 3,226 | 3,333 |
| 1979 | 3,103 | 4,125 | 3,4 | 5,374 | 6,951 | 7,055 | 6,25 | 4,301 |
| 1980 | -2,913 | -3,382 | 0 | 0 | 4,822 | 4,603 | -1,961 | 3,093 |
| 1981 | -1,7 | 2,7 | -2,6 | -1,7 | -2,3 | 1 | 1 | 3 |
| 1982 | 1,729 | -8,179 | -1,7 | -3,357 | -1,535 | 0,396 | -9,901 | 2,913 |
| 1983 | 3,2 | 6,469 | 0,9 | 0,842 | -5,613 | 3,649 | 6,593 | 4,717 |
| 1984 | -1,163 | 9,562 | 3,5 | 3,34 | 4,626 | 8,468 | 12,371 | 3,604 |
| 1985 | 5,882 | 1,818 | 1 | 5,051 | 2,105 | 3,509 | 5,505 | 3,478 |
| 1986 | 2,778 | 0,893 | 0 | 2,885 | 3,093 | 0 | 0 | 5,042 |
| 1987 | 2,703 | 5,31 | 2 | 0 | 4 | 3,39 | 4,348 | 3,2 |
| 1988 | 3,509 | 5,042 | 4,9 | 3,738 | 5,769 | 9,836 | 4,167 | 3,876 |
| 1989 | 0,847 | 2,4 | 3,7 | 5,405 | 3,636 | 5,97 | 2,4 | 1,493 |
| 1990 | -0,84 | 1,563 | 1,8 | 5,128 | 0 | 4,225 | 0 | -0,735 |
| 1991 | -2,542 | -2,308 | 0 | 2,439 | -1,754 | 1,351 | -0,781 | -8,148 |
| 1992 | -0,87 | 1,575 | 0 | -1,587 | -0,893 | -6 | 0,787 | |
| 1993 | 6,14 | 2,326 | -2,6 | -8,871 | -0,901 | -4,965 | 1,563 | |
| 1994 | 4,959 | 6,061 | 3,6 | 4,425 | 5,455 | 1,493 | 3,846 | |
Аналитические расчеты осуществлялись с помощью пакета прикладных программ математической статистики “Statistica for Windows”. Уже на этапе исследования рядов, представленных в данной таблице, удалось получить весьма неожиданные и интересные результаты:
- Спектральный анализ 1 позволил выявить наличие циклических движений в динамике промышленного производства в России. К выводу о наличии в отечественной экономике “длинной волны” можно было прийти с помощью чисто логически-исторического анализа (известные процессы индустриализации в конце двадцатых годов, замедление темпов роста и необходимость модернизации в конце семидесятых достаточно хорошо описаны в экономической литературе). Кроме того, известен также “эффект последних лет пятилетки”, когда темпы роста в двух последних годах снижались по сравнению с первыми, что также обнаруживается на приведенных графиках. Однако периодограмма показывает также пик, соответствующий примерно двадцатилетнему циклу (так называемые строительные циклы, или циклы Кузнеца, известные в капиталистической экономической динамике (см. Приложение 1).
- Исследование взаимозависимостей рядов показывает, что они обнаруживают достаточно сильную корреляцию друг с другом (см. Приложение 2). Этот расчет сделан с помощью корреляционной матрицы, и промышленное развитие России, если исходить исключительно из этого расчета, не обнаруживает корреляции ни с одним рядом показателей выпуска промышленной продукции в других странах. Тем не менее, если сузить состав стран, для которых строится матрица коэффициентов корреляции, такого рода взаимозависимости появляются для России (см. Приложение 2), в отношении же степени взаимозависимости развития других стран между собой ситуация меняется.
- Определенное противоречие, зафиксированное расчетами по п. 2, дополняется результатами исследования перекрестной корреляции рассматриваемых динамических рядов. Перекрестная корреляция позволяет выявить взаимосвязи периодических колебаний в различных рядах данных. В нашем случае сильная перекрестная корреляция с лагом, равным нулю, означает, что динамика объемов выпуска промышленной продукции в различных странах совпадает. Рассматриваются значения лага в промежутке [-15; +15] лет, соответственно, если лаг отличен от нуля, это означает, что периодические колебания объемов выпуска промышленной продукции в различных странах происходят с разницей во времени.
В связи с этим обращает внимание на себя тот факт, что в экономическом развитии различных стран нет транзитивности: другими словами, две страны, имеющие одинаковый лаг и обнаруживающие сильную перекрестную корреляцию друг с другом, могут показывать различную степень зависимости и (что может быть, даже важнее), различное значение лага при расчете перекрестной корреляции с третьей страной (см. Приложение 3). Лаги в перекрестной корреляции между рядами Великобритании и США равны нулю и –3, что означает довольно большую степень синхронности экономических процессов, имевших место в этих странах в ХХ–ом веке. Лаги между Великобританией и Германией равны –8, –7, –6, –4, +2. Наконец, лаги между процессами в Германии и США равны +2 и +15.
Что означают эти несовпадения? На данном этапе исследования мы не можем однозначно ответить на этот вопрос. В то же время само наличие высокой степени перекрестной корреляции между динамическими рядами показателей экономического развития различных стран представляется весьма важным.
Второй частью работы над выдвинутой выше гипотезой был анализ длинных волн в рассматриваемых рядах. Как ни странно, однако имеющиеся статистические данные, строго говоря, не позволяют говорить о наличии длинных волн в экономическом развитии с полной уверенностью.
Начнем с анализа динамики цен, в которой в свое время выявил большие циклы конъюнктуры сам Н. Д. Кондратьев. Исходные данные для анализа приведены в Таблице 10.
Таблица 10. Темпы прироста цен (темпы инфляции), рассчитанные на основе индекса потребительских цен по странам (1900 – 1994)
| | Англия | США | Франция | Германия | Италия | Япония | Канада | Россия |
| 1900 | 0 | 0 | 0 | 1,32 | 0 | 0 | | 0,09 |
| 1901 | 0 | 3,96 | 0 | 0 | 0 | 0 | | 0,91 |
| 1902 | 0 | 3,81 | 0 | 0 | 0 | 0 | | 2,85 |
| 1903 | 0 | 0 | 0 | 1,3 | 0 | 0 | | 2,74 |
| 1904 | 0 | 0 | 0 | 3,85 | 0 | 16,67 | | |
| 1905 | 0 | 0 | 0 | 6,17 | 20 | 0 | | |
| 1906 | 5,13 | 3,67 | 0 | 1,16 | 0 | 14,29 | | |
| 1907 | 0 | -3,54 | 0 | 0 | 0 | -12,5 | | |
| 1908 | 0 | 0 | 0 | 2,3 | 0 | 0 | | |
| 1909 | 0 | 3,67 | 0 | 2,25 | 0 | 0 | | |
| 1910 | 4,88 | 0 | 8,33 | 3,3 | 0 | 0 | | |
| 1911 | 0 | 3,54 | 0 | 5,32 | 0 | 14,29 | | |
| 1912 | 0 | 2,56 | 0 | 0 | 0 | 0 | | |
| 1913 | 0 | 1,67 | 0 | 3,03 | 0 | -12,5 | | |
| 1914 | 25,58 | 8,2 | 15,38 | 25,49 | 16,67 | 0 | | |
| 1915 | 14,81 | 17,42 | 20 | 31,25 | 28,57 | 28,57 | | |
| 1916 | 24,19 | 18,06 | 16,67 | 48,81 | 33,33 | 22,22 | | |
| 1917 | 12,99 | 14,75 | 28,57 | 19,6 | 41,67 | 36,36 | | |
| 1918 | 9,2 | 15,71 | 25,93 | 37,29 | 0 | 20 | | |
| 1919 | 13,68 | -10,7 | 38,24 | 145,68 | 35,29 | 11,11 | | |
| 1920 | -10,19 | -6,45 | -12,77 | 31,63 | 17,39 | -20 | | |
| 1921 | -18,56 | 1,97 | -4,88 | -61,96 | 0 | 75 | | |
| 1922 | -2,53 | 0 | 12,82 | 0 | 0 | -7,14 | | 57,98 |
| 1923 | 0 | 2,9 | 13,64 | -74,95 | 3,7 | 0 | | 9,57 |
| 1924 | 0 | 0,94 | 6 | 9,88 | 10,71 | 0 | | 4,37 |
| 1925 | -2,6 | -1,86 | 30,19 | 1,08 | 9,68 | -11,54 | | 9,3 |
| 1926 | -4 | -1,42 | 4,35 | 4,27 | -8,82 | -4,35 | | |
| 1927 | 0 | 0 | 0 | 3,07 | -6,45 | 0 | | |
| 1928 | 0 | -2,88 | 6,94 | 0,99 | 3,45 | -4,55 | | |
| 1929 | -5,56 | -8,42 | 1,3 | -3,61 | -3,33 | -14,29 | | |
| 1930 | -5,88 | -10,27 | -3,85 | -8,16 | -10,34 | -11,11 | -16,88 | |
| 1931 | -3,13 | -5,42 | -9,33 | -11,48 | -3,85 | 0 | -6,77 | |
| 1932 | 0 | 3,18 | -4,41 | -2,09 | -4 | 6,25 | 0 | |
| 1933 | 0 | 2,47 | -3,08 | 2,56 | -4,17 | 0 | 7,26 | |
| 1934 | 0 | 1,2 | -7,94 | 1,67 | 0 | 5,88 | 0 | |
| 1935 | 3,23 | 3,57 | 6,9 | 1,23 | 8,7 | 5,56 | 3,76 | |
| 1936 | 3,12 | -2,3 | 25,81 | 0,4 | 8 | 5,26 | 13,77 | |
| 1937 | 3,03 | -1,18 | 12,82 | 0,4 | 7,41 | 15 | -7,01 | |
| 1938 | 2,94 | 1,19 | 6,82 | 0,4 | 6,9 | 13,04 | -4,11 | |
| 1939 | 12,86 | 5,29 | 17,02 | 3,2 | 16,13 | 15,38 | 10 | |
| 1940 | 10,13 | 10,61 | 18,18 | 2,33 | 13,89 | 3,33 | 7,79 | |
| 1941 | 6,9 | 6,06 | 23,08 | 2,65 | 17,07 | 3,23 | 6,63 | |
| 1942 | 4,3 | 1,43 | 25 | 1,11 | 66,67 | 6,25 | 4,52 | |
| 1943 | 0 | 0 | 20 | 2,19 | 325 | 17,65 | 2,7 | |
| 1944 | 4,12 | 2,35 | 45,83 | 3,93 | 97,06 | 50 | 1,05 | |
| 1945 | 4,95 | 8,72 | 54,29 | 10,31 | 19,4 | 466,67 | 4,69 | |
| 1946 | 5,66 | 14,35 | 50 | 6,54 | 61,25 | 114,71 | 19,4 | |
| 1947 | 5,36 | 7,75 | 58,02 | 14,91 | 6,2 | 82,19 | 18,33 | |
| 1948 | 3,39 | -1,03 | 12,5 | 6,36 | 1,46 | 31,58 | 2,82 | |
| 1949 | 2,46 | 1,04 | 9,72 | -5,98 | -1,44 | -6,86 | 6,51 | |
| 1950 | 8,8 | 6,85 | 17,09 | 7,38 | 9,49 | 16,56 | 13,5 | |
| 1951 | 9,56 | 3,21 | 11,89 | 1,9 | 4 | 4,74 | -6,23 | |
| 1952 | 3,36 | 0,62 | -1,93 | -1,86 | 2,56 | 7,04 | -2,11 | |
| 1953 | 1,3 | 0,62 | 0 | 0 | 2,5 | 6,1 | -1,85 | |
| 1954 | 5,13 | -0,31 | 0,99 | 2,13 | 2,44 | -0,88 | 0,94 | |
| 1955 | 4,88 | 1,54 | 4,88 | 1,16 | 2,98 | 0,45 | 1,25 | 0 |
| 1956 | 3,49 | 3,33 | 2,79 | 2,98 | 1,16 | 3,11 | 3,08 | 0 |
| 1957 | 3,37 | 4,4 | 14,93 | 2,23 | 2,86 | -0,43 | 2,99 | 2,08 |
| 1958 | 0,54 | -1,69 | 6,3 | 0,87 | 0 | 0,87 | 1,16 | 1,02 |
| 1959 | 1,08 | 1,14 | 3,7 | 1,08 | 1,67 | 3,86 | 0,86 | 0 |
| 1960 | 3,21 | 1,13 | 2,86 | 2,78 | 2,73 | 4,96 | 1,14 | 1,03 |
| 1961 | 4,15 | 0,84 | 0 | 2,7 | 4,26 | 7,09 | 0,84 | 1,04 |
| 1962 | 1,99 | 1,66 | 5,56 | 3,04 | 7,65 | 7,35 | 1,95 | 1,03 |
| 1963 | 3,41 | 1,36 | 2,96 | 1,96 | 5,69 | 4,11 | 1,91 | 0 |
| 1964 | 4,72 | 2,15 | 2,88 | 3,85 | 4,93 | 6,58 | 2,41 | 1,02 |
| 1965 | 4,05 | 4,74 | 2,8 | 3,9 | 1,71 | 5,25 | 3,66 | 0 |
| 1966 | 2,16 | 1,01 | 2,42 | 1,07 | 4,62 | 3,81 | 3,54 | 0 |
| 1967 | 4,66 | 3,73 | 4,72 | 2,12 | 1,2 | 5,37 | 4,39 | 0 |
| 1968 | 5,67 | 5,04 | 6,48 | 2,08 | 1,98 | 9,38 | 4,44 | 0 |
| 1969 | 6,13 | 5,48 | 5,29 | 3,22 | 5,45 | 3,68 | 3,13 | 0 |
| 1970 | 9,39 | 3,03 | 6,03 | 4,93 | 5,17 | -0,71 | 2,82 | 0 |
| 1971 | 7,26 | 4,41 | 5,69 | 5,79 | 5,61 | 0,71 | 2,11 | 0 |
| 1972 | 9,23 | 14,49 | 7,17 | 7,1 | 10,63 | 15,84 | 10,33 | 0 |
| 1973 | 16,06 | 14,24 | 14,23 | 6,77 | 18,92 | 33,06 | 11,24 | 0 |
| 1974 | 24,03 | 8,46 | 11,54 | 6,34 | 16,92 | 11,81 | 10,1 | 0 |
| 1975 | 16,44 | 3,12 | 9,85 | 3,65 | 17,06 | 9,33 | 7,8 | 0 |
| 1976 | 15,97 | 6,33 | 8,97 | 4,34 | 18,45 | 8,03 | 7,8 | 0 |
| 1977 | 8,26 | 7,37 | 9,33 | 2,7 | 11,84 | 3,83 | -3,95 | 1,03 |
| 1978 | 13,52 | 10,96 | 10,41 | 3,94 | 14,76 | 3,58 | 24,66 | 1,02 |
| 1979 | 17,92 | 8,58 | 13,64 | 5,37 | 21,36 | 7,99 | 9,89 | 1,01 |
| 1980 | 11,9 | 10,4 | 13,5 | 5,9 | 19,5 | 4,9 | 12 | 1 |
| 1981 | 8,58 | 6,07 | 11,89 | 5,38 | 16,49 | 2,67 | 11,61 | 3,96 |
| 1982 | 4,61 | 3,25 | 9,61 | 2,96 | 14,66 | 1,86 | 5,6 | 0 |
| 1983 | 4,64 | 4,22 | 7,04 | 2,7 | 9,02 | 2,1 | 4,55 | 0,95 |
| 1984 | 6,77 | 3,97 | 6,04 | 2,54 | 9,2 | 1,79 | 3,62 | 0,96 |
| 1985 | 2,82 | 1,53 | 2,53 | 0 | 6,32 | 0,88 | 4,2 | 1,9 |
| 1986 | 4,11 | 3,76 | 3,09 | 0 | 4,46 | 0 | 4,03 | 0,93 |
| 1987 | 5,26 | 4,35 | 2,99 | 1,65 | 5,21 | 0,87 | 4,52 | 1,85 |
| 1988 | 7,5 | 4,86 | 3,49 | 2,44 | 6,31 | 2,59 | 4,94 | 1,81 |
| 1989 | 9,88 | 5,3 | 3,37 | 2,38 | 6,36 | 2,52 | 4,71 | 5,36 |
| 1990 | 5,82 | 3,77 | 3,26 | 3,88 | 6,37 | 3,28 | 5,62 | 0 |
| 1991 | 3,5 | 3,03 | 2,11 | 3,73 | 4,87 | 2,38 | 1,6 | 1528,81 |
| 1992 | 2,27 | 3,82 | -1,34 | 12,3 | 4,89 | 0,23 | 1,57 | 874,25 |
| 1993 | 1,79 | 1,81 | 0,94 | -15,95 | 3,4 | 0,93 | 0 | 307,65 |
Попытка получить “длинные волны” с помощью процедуры экспоненциального сглаживания с устранением девятилетних “сезонных колебаний” (циклов Жуглара) позволяет говорить, с некоторой долей сомнения, о циклах в экономическом развитии Англии, США, Франции; и явно не выдерживает критики, когда речь идет о Японии и Германии (см. Приложение 4). Процедура спектрального анализа не обнаружила длинных волн в рядах приростов цен, что ставит перед исследователями трудные вопросы. Однако небезынтересно отметить, что и в отечественной экономической литературе по вопросам статистической проверки наличия длинны волн в экономической литературе существует определенная разноголосица: С. М. Меньшиков и Л. А. Клименко выступают против применения “рафинированных математических методов типа спектрального анализа и более склонны на первоначальном этапе исследования к простым процедурам, которые применял еще Н. Д. Кондратьев, а также визуальному анализу, который всегда давал богатый материал для формулирования гипотез” 2. Напротив, в авторитетной коллективной монографии 3 применению данного метода исследования посвящена целая глава, приводятся результаты анализа, в соответствии с которым обнаружены длинные волны в рядах приростов патентов, в движении индекса цен производителей. (С другой стороны, в данной монографии авторы указывают, что им не удалось с помощью спектрального анализа выделить волны в индексе промышленного производства в США 4. Однако нам удалось сделать это в отношении темпов прироста промышленного производства (см. Приложение 1.) Однако проблему представляет то обстоятельство, что этого не удалось сделать в отношении некоторых других стран, в первую очередь, Англии.) В свою очередь, переход к понижательной фазе волны цикла Кондратьева во второй половине ХХ-го века связывается большинством исследователей с кризисом 1973 – 1982 гг., однако в это время во многих развитых странах мира имело место явление стагфляции, что затрудняет традиционный анализ конъюнктуры. Нельзя не заметить, что на большинстве графиков для визуального анализа, приведенных С. М. Меньшиковым и Л. А. Клименко, этот переход к понижательной волне цикла либо отсутствует, либо его дата относится к значительно более раннему периоду 5.
Таким образом, попытка выявления длинных волн в настоящий момент в нашем исследовании принесла противоречивые результаты. Хотя наличие циклов Кондратьева в экономической динамике с очевидностью обнаруживается при рассмотрении смены поколений техники, характера экономического развития, выражающегося в широко известном снижении темпов роста ряда макроэкономических показателей (темпы прироста ВВП, производительности труда, реальных доходов на душу населения и т.д.), структурных сдвигов (переход к “постиндустриальной” экономике, где ключевую роль играет сфера услуг) — несмотря на все эти убедительные свидетельства, с точки зрения количественного анализа наблюдаемых тенденций говорить о реализации закономерностей длинных волн в экономическом развитии приходится по-прежнему с большой осторожностью.
1 Спектральный анализ позволяет выявить в динамических рядах процессы различной длительности. В его основу положено то обстоятельство, что любой конечный дискретный процесс можно представить разложением в ряд Фурье в виде суммы синусов и косинусов, совпадающей в каждой точке со значением исходного ряда.
2 Меньшиков С.М., Клименко Л.А. Длинные волны в экономике. Когда общество меняет кожу. - М.: Международные отношения, 1989. - С. 66.
3 Длинные волны: Научно-технический прогресс и социально-экономическое развитие. С.Ю. Глазьев, Г.И. Микерин, П.Н. Тесля и др. - Новосибирск: Наука. Сиб. отд-е, 1991. -См. с. 186 - 203.
4 Там же, с. 202.
5 Меньшиков С.М., Клименко Л.А. Длинные волны в экономике. - С. 72 - 75.
|